[Statistics 1] 몬테 카를로 시뮬레이션 (Monte Carlo Simulation)
- 작성자 : 통실돼지
- 일자
- 게재: 2022-05-13
- 수정: 2022-05-14
1. 서론
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle.
해석: 광범위한 계산 알고리듬의 일종인데, 특히 반복적인 랜덤 샘플링에 의존하여 결과를 얻는 것이다. 문제를 풀기 위해 (그 문제가 결정론적인 원리라고 하더라도) 무작위성을 이용한다.
몬테 카를로 시뮬레이션 예시로 꼭 나오는 “원주율값 구하기“를 직접 하면서, 몬테 카를로 시뮬레이션이 무엇인지, 어떻게 사용되는지, 그리고 효율성이 있는지를 알아 보도록 하겠습니다.
2. 반지름이 1인 원의 넓이 계산하기
모두가 알듯 원의 넓이는 $\pi r^2$ 이며 $r=1$ 이므로, 정답은 $\pi$, 약 3.1415 입니다.
2.1. 결정론적인 방법 - 부정적분 활용하기
원의 넓이를 구하는 결정론적인 방법은 부정적분을 활용하는 것입니다.
그 방법은 1 사분면에서 넓이를 먼저 계산한 이후 4를 곱합니다.
그 과정에서 역삼각함수를 이용하면 부정적분을 계산할 수 있고 간단하게 값이 $\pi$ 가 됨을 확인할 수 있습니다.
\begin{aligned} S = \pi = 4\int_{0}^{1}\sqrt{1-x^2}dx \end{aligned}
2.2. 시뮬레이션 활용 방법
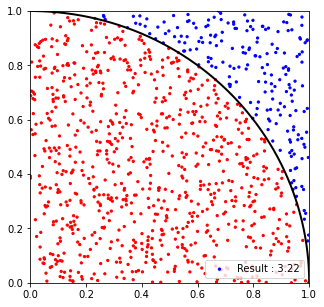
시뮬레이션을 활용하여 원의 넓이를 구하는 방법은 영역 내 수 많은 점을 찍어보는 것입니다.
가로와 세로의 길이가 1인 정사각형 안에 하나의 점을 무작위로 고른다고 가정합시다.
그 때, 해당 점이 붉은색이 될 확률은 전체 영역 대비 붉은색 영역의 넓이와 같습니다.
그리고 그 영역의 계산은 찍은 점의 개수로 대신하게 됩니다.
따라서, 무작위로 한 점을 선택했을 때 이 점이 붉은색 영역에 속한 점이 될 확률은 전체 점의 개수 대비 빨간색 점의 개수가 될 것입니다.
\begin{aligned}
붉은색\,영역이\,선정될\,확률\,=\frac{빨간색\,영역\,넓이}{전체\,영역\,넓이}\,\approx\frac{빨간색\,점\,개수}{전체\,점\,개수}
\end{aligned}
만일 우리가 무작위로 점을 선택(찍는) 과정을 수없이 반복한다면, 확률의 큰 수 법칙에 따라서 전체 점의 개수 대비 빨간색 점 개수의 비율은 거의 $\pi/4$에 근접하게 됩니다.
\begin{aligned} \frac{빨간색\,점\,개수}{전체\,점\,개수}\,=\,\pi/4 \end{aligned}
2.2.1 실습
아래는 상기 문제에 대한 몬테카를로 시뮬레이션의 실습 코드입니다.
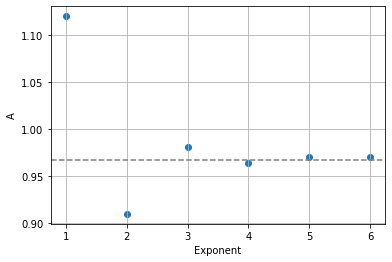
결과를 보면, 시행 $N$이 커질수록 결과 값이 실제 원주율값에 가깝에 얻어지고 각 시행의 편차가 작아집니다.
이는 확률과 통계에 대한 우리의 기본적인 직관과 일치합니다.
더 많은 시행을 반복할수록 정답 값에 수렴하게 됩니다.
- 반지름 1인 원의 넓이 구하기
- $N=1000$
# 필요한 라이브러리 불러오기
import numpy as np
from multiprocessing import Pool
from matplotlib import pyplot as plt
if __name__ == '__main__':
N = 1000 ### 무작위시행 횟수 정의
x = np.random.random([N, 2])
distance = np.sum(x ** 2.0, axis=1)
in_out = distance <= 1.0
pi = np.sum(in_out)/N*4 ### Pi 값은 전체 시행에서 원 안에 있는 점의 갯수로 정해짐
color = list(map(lambda x: 'red' if x else 'blue', in_out)) ### 원의 안, 밖에 따른 색상 설정
plt.figure(figsize=(5, 5)) ### 그림 사이즈
plt.scatter(x[:,0], x[:,1], color = color, s=5, label ='Result : {}'.format(np.round(pi, 4)))
cx = np.cos(np.linspace(0, np.pi/2, 1000))
cy = np.sin(np.linspace(0, np.pi/2, 1000))
plt.plot(cx, cy, color = 'black', lw =2) ### 원의 경계를 그려주는 부분
plt.legend(loc = 'lower right')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.show()
- 임의 함수의 적분 면적 구하기
- $N=10000$
import numpy as np
from matplotlib import pyplot as plt
def function(x): ### 함수 정의
return x**2 + np.sin(np.pi*x)
if __name__ == '__main__':
N = int(1e+4) ### 랜덤 샘플링 시행 횟수 정의
W, H = 1, 1.4 ### 랜덤 샘플링을 할 사각형 R의 가로 세로 정의
X = np.random.random(N) ### 각 점의 x 좌표 랜덤 샘플링
Y = H*np.random.random(N) ### 각 점의 y 좌표 랜덤 샘플링
F = function(X) ### 각 랜덤 샘플링에 대한 f(x)를 계산
in_out = Y < F ### y와 f(x) 값 비교
A = H * W * np.sum(in_out) / N ### 영역 S의 넓이
print("A = ", A)
color = list(map(lambda x: 'dodgerblue' if x else 'red', in_out))
### 샘플링 포인트의 색깔 설정
plt.scatter(X, Y, color=color, s=5, label='A = {}'.format(np.round(A, 4)))
### 샘플링 포인트 그리기
plt.plot([0, W], [0, 0], color='black') ### 사각형 영역 그리기
plt.plot([W, W], [0, H], color='black')
plt.plot([0, W], [H, H], color='black')
plt.plot([0, 0], [0, H], color='black')
px = np.linspace(0, W, 1000)
py = function(px)
plt.plot(px, py, color = 'black') ### 함수 y = f(x) 그리기
plt.legend(loc = 'lower right') ### 그래프 그리는 옵션 추가
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
A = 0.96334
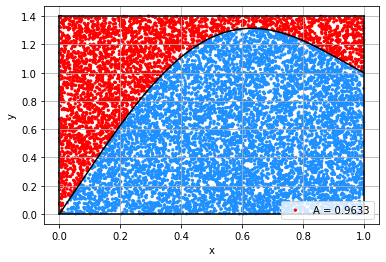
- 임의 함수의 적분 면적 구하기
- 시행 횟수에 따른 결과 값을 나타내면 다음과 같습니다.
- $N=10, 100, 1000, 10000, 100000, 1000000$
if __name__ == '__main__':
N = int(1e+4)
W, H = 1, 1.4
As = []
for d in [1, 2, 3, 4, 5, 6]: ### 10^{1, 2, 3, 4, 5, 6}에 대한 계산 반복
N = 10**d
X = np.random.random(N)
Y = H*np.random.random(N)
F = function(X)
in_out = Y < F
A = H * np.sum(in_out) / N ### 넓이를 계산
As.append(A) ### 계산된 넓이를 As에 저장
plt.scatter([1, 2, 3, 4, 5, 6], As) ### d에 따른 A값을 그리기
plt.xlabel('Exponent')
plt.ylabel('A')
plt.axhline(0.967, color='gray', ls='--') ###참값 표시
plt.grid()
plt.show()
- 주의사항
- 수 많은 반복 이후 실제 정답 값과 비슷한 값을 얻는다는 것을 명심해야 합니다.
- 점을 선택하는 과정이 가로 $\times$ 세로의 길이가 1인 정사각형 내 모든 점을 정말로 무작위적이고 고르게 뽑아야 합니다.
- 특정 영역의 점을 많이 뽑거나 혹은 반대로 특정 영역의 점을 적게 뽑는다면, 정답과 비슷한 결과가 나오지 않을 수 있습니다.
3. 마무리하며
- 결과
- 몬테카를로 시뮬레이션이란 무작위 반복 시행을 활용하여 참 값을 유추하는 방법론임을 알 수 있었습니다.
- 결론
- 더 빠르게 최적점을 도출해낼 수 있다면 그 활용도가 높을 것입니다.
참고 자료
[1] https://studyingrabbit.tistory.com/33
[2] https://studyingrabbit.tistory.com/34
[3] https://studyingrabbit.tistory.com/35
그 외
- J. Choi!
댓글남기기