5 분 소요

  • 작성자 : 통실돼지
  • 일자
    • 게재: 2022-12-28
    • 수정: 2023-01-09

분산분석 (ANalysis Of VAriance, ANOVA) 1 - 개요

0. 시작하기에 앞서 (Before the beginning)

  • 본 시리즈 (series)는 통계분석 기법 중 하나인 분산분석 (ANalysis Of VAriance, ANOVA)에 관한 것입니다.
  • ANOVA는 두 개 이상의 집단을 통계적으로 비교하기 위한 방법 중 하나입니다.
  • 더 자세한 내용이 궁금하신 분들은 공학자와 과학자를 위한 확률과 통계, 그리고 신뢰성에 관한 서적을 참고하시면 됩니다[1].

1. ANOVA 란?

1.1 개념

ANOVA는 통계학에서 두 개 이상의 다수 집단의 평균이 서로 간 유의한지 판단하고자 할 때 사용합니다[2, 3].

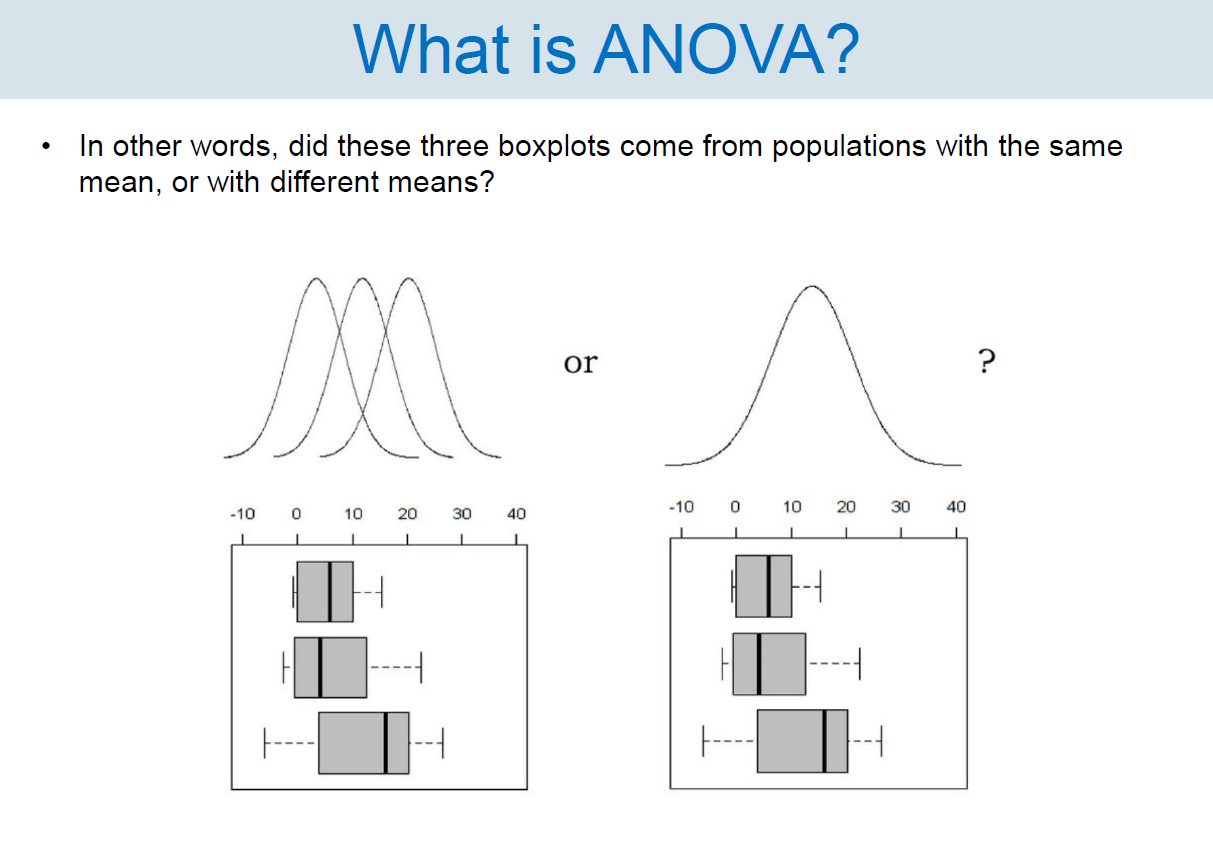fig_1 [동일한 모집단에서 온 것인가?] (부산대학교 노유정 교수님 “확률 및 통계” 수업자료 중 일부) [4]

특히, 집단 내의 분산과 집단 간의 분산, 그리고 F-분포 (F-distribution)를 이용하여 각 집단 별 평균에 대한 유의성을 확인하게 됩니다.

fig_2 [집단 내 분산 (within group variance)과 집단 간 분산(between group variance)] (부산대학교 노유정 교수님 “확률 및 통계” 수업자료 중 일부) [4]

두 개의 집단 간 차이를 비교할 때에는 T-test를 사용하므로, 세 집단 간 평균의 차이를 비교할 때 T-test를 3번 수행하는 방법을 떠올릴 수 있습니다.

하지만 이 경우 실제로 유의하지 않은데 유의하다고 나오는 1종 오류에 걸리게 됩니다[5]. 5% 유의 수준을 기준으로 3번의 T-test를 수행하면, $5 \%$를 세 번 적용하므로 총 유의수준은 $0.05 \times 3=0.15$가 되어 1종 오류에 빠지기 쉽습니다.

따라서 3개 집단 이상을 비교할 때 일반화된 T-test가 필요하게 되는데, 이때 ANOVA를 활용하면 상기 문제를 해결할 수 있습니다[6]. 문제에 ANOVA를 적용하기 이전에, T-test와 마찬가지로 등분산성, 정규성, 독립성의 조건이 전제되어야 합니다[7].

  • 정규성 가정: 각 그룹에서 표본은 정규성을 띔.
  • 등분산성 가정: 각 집단의 분산은 서로 동일해야 함.
  • 독립성 가정: 표본은 서로 독립적이어야 함.

1.2 종류

ANOVA는 요인 (factor, independant variable)과 반응변수 (response variable, dependant variable)의 개수에 따라 다음과 같이 나눌 수 있습니다[7].

  • 일원 분산 분석 (One-way ANOVA): 요인 1개 & 반응변수 1개
  • 이원 분산 분석 (Two-way ANOVA): 요인 2개 & 반응변수 1개
  • 다변량 분산 분석 (One-way Multiple ANalysis Of VAriance(MANOVA), Two-way MANOVA): 요인 1개 & 반응변수 2개, 요인 2개 & 반응변수 2개
  • 공 분산 분석 (ANalysis of COVAriance(ANCOVA)): 요인 & 공변량 요인 & 반응변수

문제의 상황에 맞는 ANOVA 풀이법을 적용해야 합니다.

1.3 장점 및 단점

ANOVA의 장점과 단점은 다음과 같습니다[8].

  • 장점
    1. ANOVA를 활용하면 서로 다른 두 개 이상의 집단 평균 간 차이를 정량적으로 평가할 수 있음.
    2. 집단 내 오차에 의한 차이인지 정량적으로 평가할 수 있음.
    3. 2번과 비슷한 맥락으로, 요인이 반응 변수에 영향을 미치는지 간접적으로 보여줌.
  • 단점
    1. 최소 두 그룹의 평균 간 유의한 차이가 있는지 여부를 확인할 수 있으나, 어떤 쌍에서 유의한 차이가 발견되었는지 설명할 수 없음.
    2. 데이터의 분포가 정규적이지 않고, 특이치가 존재하는 경우 적합하지 않음.
    3. 데이터의 표준 편차가 그룹간 동일하거나 유사하지 않은 경우 적합하지 않음.

2. ANOVA의 계산 방법?

2.1 계산 방법의 개요

일원 분산분석 (ANOVA)의 계산은 다음과 같이 6단계로 구성됩니다[1, 4].

  • Step 0. 가정 확인 - 정규성, 등분산성, 독립성
  • Step 1. 가설 세우기 (Formulation of hypothesis)
  • Step 2. 평가할 통계량과 그 분포의 정의 (Define the test statistic and its distribution)
  • Step 3. 유의수준 정의 (Specify the level of significance) ANOVA Table 계산
  • Step 4. 데이터 획득 & 평가 통계량 계산 (Collect data and compute test statistic) ANOVA Table 계산
  • Step 5. 평가 통계량의 임계값 결정 (Determine the critical value of the test statistic) ANOVA Table 계산
  • Step 6. 결정 내리기 (Make a decision)

2.2 Step 0. 가정 확인

일원분산분석에서는 분석 이전에 다음의 3 가지 가정을 확인해야 합니다[4, 9].

1) 정규성 가정

  • 의미: 각 변수는 정규 분포를 따라야 함.
  • 방법: Shapiro test
  • 가설:
    • H0: 변수는 정규 분포를 따름.
    • H1: 변수는 정규 분포를 따르지 않음.
  • 그 외
    • Shapiro test는 p-value가 보수적으로 나오므로, 실무적으로는 변수의 왜도값이 2를 넘지 않으면 보통 시험을 실시함.

2) 등분산성 가정

  • 의미: 각 변수의 분산은 동일한 수준의 분산을 가져야 함.
  • 방법: Barlett or Levene test
  • 가설:
    • H0: 변수 간 분산에 유의한 차이가 존재하지 않음.
    • H1: 변수 간 분산에 유의한 차이가 존재함.

3) 독립성 가정

  • 의미: 그룹 간 서로 영향을 주고 받으면 안됨.
  • 방법: -
  • 그 외:
    • 통계적인 숫자로 확인하기 보다는, 실험 설계에서 결정되어야 함.

2.3 Step 1. 가설 세우기

k 개의 표본집단을 비교할 때, 가설은 k 개의 표본집단의 평균을 비교하게 됩니다.

  • $H_0$: 표본 $\mu_1$과 $\mu_2$, …, $\mu_k$는 서로 유의하지 않음.
    \begin{aligned} H_0: mean(\mu_1) = mean(\mu_2) = … = mean(\mu_k) \end{aligned}

  • $H_1$: 표본 s1과 s2, s3 중 어느 하나라도 유의한 것이 있음.
    \begin{aligned} H_1: not\,H0 = at\,least\,one\,pair\,of\,group\,means\,are\,not\,equal \end{aligned}

2.4 Step 2. 평가할 통계량과 그 분포의 정의

다음의 F 통계량을 확인하여 상기 가설을 검정할 수 있습니다.

\begin{aligned} F = \frac{MS_b}{MS_w} \end{aligned}

$MS_b$: 군간 평균 제곱합,
$MS_w$: 군내 평균 제곱합,
$F$ 통계량: $(k-1, N-k)$ 자유도의 $F$ 분포를 갖는 확률 변수 (random variable)

$MS_b$, $MS_w$ 는 다음의 ANOVA Table을 계산함으로써 구할 수 있습니다.

fig_3
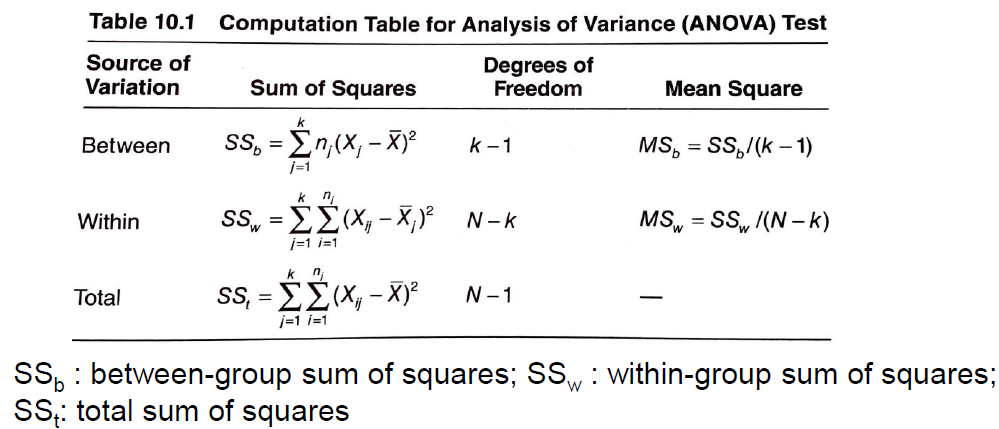
[일원 분산분석 위한 ANOVA Table] (부산대학교 노유정 교수님 “확률 및 통계” 수업자료 중 일부) [4]

2.5 Step 3. 유의수준 구체화

유의수준은 타 검정과 마찬가지 방식으로 사용됩니다.

2.6 Step 4. 데이터 획득 & 평가 통계량 계산

평가 통계량 $F$를 계산하기 위해 데이터를 모아야 하며, 그 예시는 아래와 같습니다.
총 $k$개 집단이 있으며, $1$ 부터 $k$개 집단 중 $j$ 번째 집단을 가정하였을 때 $j$번째 집단의 관측치 수는 $n_j$로 표기할 수 있습니다. (각 집단의 관측치 수인 $n_j$는 동일하지 않을 수 있습니다.)
전체 관측치 수인 $N$은 다음과 같이 정의됩니다.

\begin{aligned} N = \sum_{j=1}^{k} n_j \end{aligned}

fig_4
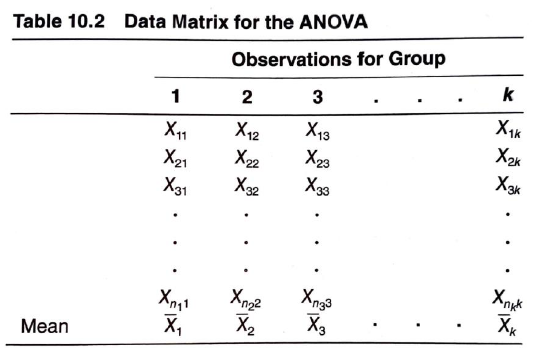
[일원 분산분석 위해 모은 데이터의 예시 표] (부산대학교 노유정 교수님 “확률 및 통계” 수업자료 중 일부) [4]

2.7 Step 5. 평가 통계량의 임계값 결정

유의수준과 자유도로부터 $F_{critical}$ 통계량이 계산됩니다.

2.8 Step 6. 결정 내리기

관측된 통계량인 $F_{observed}$와 임계 통계량인 $F_{critical}$의 비교를 통해 적절한 가설을 채택하게 됩니다.

  • $F_{critical}$보다 더 높은 영역에서 $F_{observed}$가 관측된다면, 귀무 가설(null hypothesis, $H_0$)은 기각 (reject)되고 대립 가설 (alternative hypothesis, $H_1$)이 채택 (accept)됩니다.
  • $F_{critical}$보다 더 낮은 영역에서 $F_{observed}$가 관측된다면, 귀무 가설(null hypothesis, $H_0$)은 채택 (accept)되고 대립 가설 (alternative hypothesis, $H_1$)은 기각 (reject)됩니다.

$F_{observed}$에서의 확률값과 $F_{critical}$에서의 유의수준 $\alpha$의 비교를 통해 내렸던 결정의 신뢰 정도를 확인할 수 있습니다.

  • $F_{observed}$에서의 확률값과 $F_{critical}$에서의 유의수준 $\alpha$값과 비슷하다면, 귀무 가설(null hypothesis, $H_0$)을 채택한 결정의 신뢰 정도는 비교적 낮을 것입니다.
  • $F_{observed}$에서의 확률값이 $F_{critical}$에서의 유의수준 $\alpha$값보다 월등히 클 경우, 귀무 가설(null hypothesis, $H_0$)을 채택한 결정의 신뢰 정도는 비교적 높을 것입니다.

3. 마무리하며 (Closing Remarks)

  • 많은 내용을 담기 어려워 시리즈로 기획하였습니다.
  • 첫 포스트에서는 ANOVA의 개념부터 장단점, 계산방법 등 이론적인 부분을 살펴보았습니다.
  • 다음 포스트에서는 ANOVA를 활용한 계산 실습을 진행할 예정입니다.
  • 마지막 포스트에서는 Python을 활용하여 예제에 ANOVA를 적용하는 실습을 계획하고 있습니다.

4. 참고문헌 (References)

[1] Bilal M. Ayyub, Richard H. McCuen, “Probability, Sttistics, and Reliability for Engineers and Scientists,” Link
[2] 위키백과, “분산 분석,” Link
[3] WIKIPEDIA, “Analysis of variance,” Link
[4] 부산대학교 노유정 교수님 확률및통계 수업자료
[5] YSY의 데이터분석 블로그 Tistory blog, “[기초통계학] One-way ANOVA (일원배치 분산분석) (F-Value),” Link
[6] [Alex] 데이터 장인의 블로그 Tistory blog, “데이터 분석을 위한 통계(ANOVA) feat. python,” Link
[7] BioinformaticsAndMe Tistory blog, “분산 분석 (ANOVA),” Link
[8] TIBC, “What is Analysis of Variance (ANOVA)?,” Link
[9] 데이터로 하는 마케팅 Tistory blog, “[Python] One way ANOVA 분석하기 - 이론부터 코드까지 한 번에,” Link

Etc…

  • 졸업 준비로 굉장히 오랜만에 포스팅하였습니다.
  • 블로그에 대문짝만하게 작성했던 제 다짐이 무색해졌지만, 그래도 조금씩 포스팅하겠습니다.
  • 더 열심히 하겠습니다! 부족한 부분 코멘트해주세요 (:

읽어주셔서 감사합니다!!

댓글남기기

참고