9 분 소요

  • Author : Songho Lee
  • Date
    • First Published: September 02, 2022
    • Last modified: September 06, 2022

정현파 신호 (Sinusoidal Signals)

시작하기에 앞서 (Before the beginning)

  • 파이썬을 활용한 정현파 신호의 실습을 진행하겠습니다.

  • 조금 더 자세한 내용이 궁금하신 분들은 여기를 참고하시면 됩니다.

1. 서론 (Introduction)

  • 본 실습의 목적은 앞으로 포스팅될 내용(신호처리, 머신러닝 등)의 가장 기본이 되는 정현파 및 여러 디지털 신호의 생성에 관한 것입니다.

2. 실습 (Practice)

  • 먼저 필요한 라이브러리를 불러옵니다.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

2.1. 정현파 생성하기 (Generating sinusoidal wave)

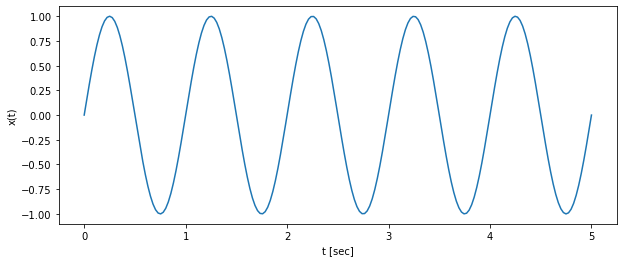
  • 간단하게 주파수($f$) 1 (= 주기($T$) 1, 주기는 주파수의 역수이므로) 이며, 그 진폭($A$)도 1인 사인파형을 생성해보겠습니다.

\begin{aligned} x(t)&= \sin(2 \pi t) \end{aligned}

  • 생성한 사인파는 아래와 같습니다.

  • 아래와 같이 한 주기에 40개의 포인트를 샘플링하는 경우, 원래 의도했던 연속적인 사인파형을 잘 나타내는 것을 확인할 수 있습니다.

t_1 = np.linspace(0,5,200)
x_1 = np.sin(2*np.pi*t_1)

# plot
plt.figure(figsize = (10,4))
plt.plot(t_1, x_1, '-')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.show()

output_11_0

​

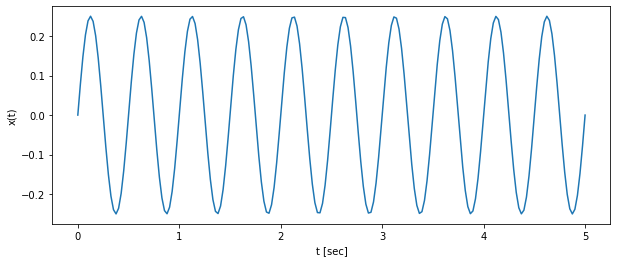
  • 이번에는 주파수($f$) 2 (= 주기($T$) 0.5) 이며, 진폭($A$) 0.25인 사인파형을 생성해보겠습니다.

\begin{aligned} x(t)&= 0.25\sin(4 \pi t) \end{aligned}

  • 주파수가 1 일때와 마찬가지로 원래 사인파를 잘 나타내는 것을 아래의 결과에서 확인할 수 있습니다.
t_2 = np.linspace(0,5,200)
x_2 = 0.25 * np.sin(2*np.pi*2*t_2)

# plot
plt.figure(figsize = (10,4))
plt.plot(t_2, x_2, '-')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.show()

output_15_0

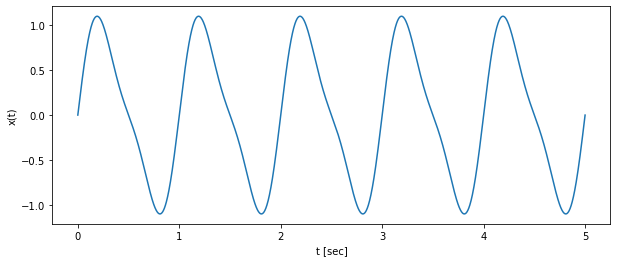
2.2. 정현파 합성하기 (Synthesizing sinusoidal wave)

  • 상기 두 신호를 더하면 어떻게 될까요?

  • 두 신호를 더한 식은 아래와 같습니다.

\begin{aligned} x(t)&= \sin(2 \pi t) + 0.25\sin(4 \pi t) \end{aligned}

t_3 = np.linspace(0,5,2000)
x_3 = np.sin(2*np.pi*t_3) + 0.25 * np.sin(2*np.pi*2*t_3)

# plot
plt.figure(figsize = (10,4))
plt.plot(t_3, x_3, '-')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.show()

output_19_0

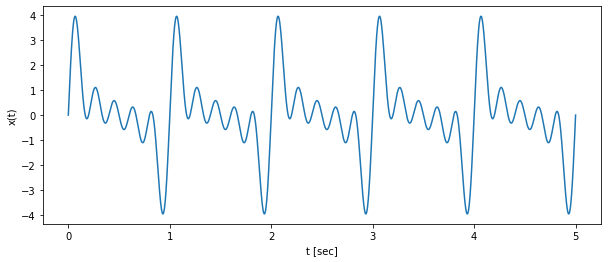
  • 이번에는 진폭은 1로 동일하며 다양한 정수배 주파수를 가진 신호를 더해서 나타내어 보겠습니다.

  • 예제 신호는 아래와 같습니다.

\begin{aligned} x(t)&= \sin(2 \pi t\times 1) + \sin(2 \pi t\times 2) + \sin(2 \pi t\times 3) + \sin(2 \pi t\times 4) + \sin(2 \pi t\times 5) \end{aligned}

t_4 = np.linspace(0,5,2000)
x_4 = (np.sin(2*np.pi*t_4 * 1)
       + np.sin(2*np.pi*t_4 * 2)
       + np.sin(2*np.pi*t_4 * 3)
       + np.sin(2*np.pi*t_4 * 4)
       + np.sin(2*np.pi*t_4 * 5))

# plot
plt.figure(figsize = (10,4))
plt.plot(t_4, x_4, '-')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.show()

output_22_0

  • 상기 예제들을 통해서, 삼각함수 파형을 더하는 경우 새롭고 다양한 모양의 파형이 형성되는 것을 확인할 수 있습니다.

  • 그 말인 즉, “여러 모양의 정현파 파형을 더함으로써, 임의의 입력 신호를 나타낼 수 있다.” 는 것을 의미합니다.

  • 푸리에 변환 (Fourier Transform)을 활용하면, “시간축 상에 나타난 임의의 비주기 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현” 할 수 있습니다.

  • 이를 통해서 시간 영역에서 관찰하기 어려운 임의의 신호를 쪼개어서, 주파수 영역에서 신호의 구성 주파수 성분을 확인할 수 있습니다.

  • 푸리에 변환에 대한 자세한 것은 다음 포스팅에서 논하도록 하겠습니다.

2.3. 정현파로 구성된 다양한 신호들 (Various signals composed with sinusoidal waves)

  • 여기서부터는 정현파로 구성할 수 있는 다양한 신호를 만들어 보겠습니다.

  • 직관적인 이해를 돕기 위해, 생성한 신호를 소리로도 들어보기 위해 다음의 라이브러리를 불러옵니다.

from scipy.io import wavfile
from IPython.display import Audio

2.3.1. 기본적인 코사인 신호 (Basic cosine wave)

  • 신호 주파수($k$), 관찰 주파수($f_o$) 인 기본적인 코사인 신호는 아래와 같습니다.

  • $f_o$를 관찰 주파수라고 한 이유는, $f_o$까지 관찰하기 위해서 $f_s$을 사용하여 $f_o$의 두 배에 해당하는 샘플링을 수행하기 때문입니다.

\begin{aligned} f_o&= f_s / 2 \end{aligned}

  • 샘플링 주파수와 신호의 주파수를 쉽게 설정할 수 있도록 코드를 변경하였습니다. 또한 그 2배를 샘플링 할 수 있도록 ($n$) 코드를 짰다는 것입니다.

  • 이렇게 2배 이상의 샘플링 레이트를 만족하면서 나이키스트 샘플링 레이트를 만족할 수 있게 됩니다.

# Cosine wave
## sampling rate
N = 44100/2
fo = N
fs = np.arange(0, 2*N)

## signal frequency
f = 40 

## signal
coswave = np.cos(2*np.pi/N*f*fs)

## plot
plt.figure(figsize = (10, 4))
plt.plot(fs/fo, coswave)
plt.show()

output_31_0

알쓸신잡

  • $f_s = 44.1kHz$는 샘플링 주파수로 많이 쓰이는데, 그 유래는 다음과 같습니다[2-4].

    1. 오디오 가청 주파수 밴드폭은 $20 - 20,000Hz$이므로, 이론상 샘플링 주파수가 $40kHz$ 이상이면 되기 때문에 정해진 것

    2. 44.1kHz의 정확한 샘플링 속도는, CD 사양이 개발될 당시 녹음 스튜디오에서 CD 제조업체로 데이터를 전송하는 가장 저렴한 방법인 PCM 어댑터에서 유래됨.

2.3.2. 첩 (Chirp)

  • 첩은 시간이 지남에 따라 주파수가 증가 (up-chirp) 혹은 감소 (down-chirp)하는 신호입니다[1,5].

  • 아래는 첩 신호의 예시입니다.

\begin{aligned} x(t)&= 0.3\cos(2 \pi f t^2) \end{aligned}

# Chirp 
N = 44100
fo = N
fs = np.arange(0,fo*2)
chirp = 0.3*np.cos(2*np.pi/3000000*fs**2)

# plot
plt.figure(figsize = (10, 4))
plt.plot(fs/fo, chirp)
plt.xlim([0, 0.4])
plt.show()

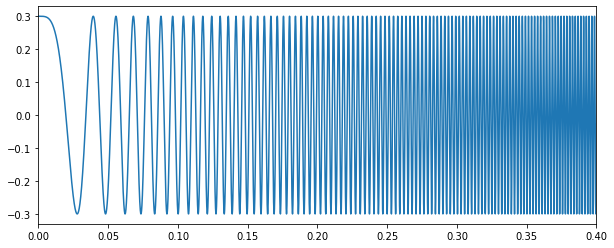
output_35_0

  • 생성한 파형을 소리로 듣게되면 다음과 같습니다.

  • 시간이 지남에 따라 점진적으로 높은 음이 나는 것을 알 수 있습니다.

  • 시끄러울 수 있으니 주의하세요!

Audio(chirp, rate = 44100)

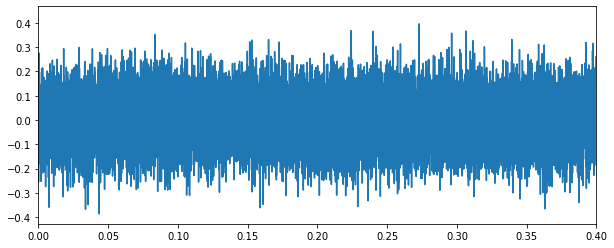
2.3.3. 백색 가우시안 잡음 (White gaussian noise)[6]

  • 백색 잡음(white noise)
    • 모든 주파수에 걸쳐서 전력 스펙트럼 밀도(power spectrum density, PSD)가 일정한 신호, 모든 주파수 영역에서 잡음이 나타난다는 것을 의미합니다.
    • 백색이라고 이름을 붙인 이유는 빛의 색을 모두 합치면 흰색이 되기 때문입니다.
    • 백색잡음은 무한한 평균전력을 갖게 되어 실현이 불가능한데, 가장 근사적인 잡음으로 열잡음(thermal nosie)이 있습니다.
    • 열잡음은 넓은 범위의 주파수에서 백색과정으로 근사하게 모델링할 수 있습니다.
    • 결국, 백색과정은 모든 주파수에서 같은 전력을 가지는 확률적 과정을 말합니다.
    • 백색 잡음 (white noise)은 가우시안 (Gaussian) 확률함수로 모델링되어 주로 AWGN(additive white Gaussian noise)에 적용됩니다.
  • 가우시안 노이즈(Gaussian noise)
    • 정규분포를 가지는 잡음, 일반적인 잡음이며 어느정도 랜덤하면서 자연계에서 쉽게 볼 수 있는 분포를 가진 잡음을 의미합니다.
  • 가산적(additive) 의미
    • 잡음이 신호에 더해지는 효과로 나타난다는 것을 의미합니다.
    • 열잡음이 가산적이라함은 신호 위에 곱하기 연산 과정 없이 단지 더해지는 형태를 취하기 때문입니다.
    • 모든 통신 채널에 항상 가산적으로 부가됩니다.
  • AWGN(additive white Gaussian noise) 채널
    • 일반적인 잡음이 있는 채널을 의미합니다.
    • 열잡음의 에너지 스펙트럼이 시간 영역에서는 가우스 분포를 가지며, 주파수 영역에서는 균일한 분포를 갖는 잡음이 됩니다.
  • np.random 기능은 다음과 같습니다[7].
    • np.random.randint: 균일 분포의 정수 난수 1개 생성
    • np.random.rand: 0부터 1사이의 균일 분포에서 난수 matrix array 생성
    • np.random.randn: 평균 0, 표준편차 1의 가우시안 표준 정규분포에서 난수 matrix array 생성
  • 백색 가우시안 잡음은 다음과 같습니다.

\begin{aligned} Noise&∼ N(0, 1^2) \end{aligned}

# white gaussian noise
N = 44100
fo = N
fs = np.arange(0,fo*2)
noise = 0.1*np.random.randn(len(fs),1) # random number matrix (2 x fo,1) 

# plot
plt.figure(figsize = (10, 4))
plt.plot(fs/fo, noise)
plt.xlim([0, 0.4])
plt.show()

output_42_0

Audio(noise.T, rate = fo)
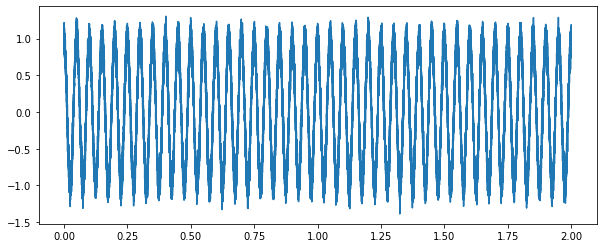
  • 기본적인 코사인 파형에 가우시안 잡음을 추가한 파형은 아래와 같습니다.

\begin{aligned}Noise&∼ N(0, 1^2)\\Signal(t)& = \cos(2 \pi f t) + Noise\end{aligned}

# Cosine wave
## sampling rate
N = 44100/2
fo = N
fs = np.arange(0, 2*N)

## signal frequency
f = 20 

## signal
signal =  np.cos(2*np.pi/N*f*fs) + 0.1*np.random.randn(len(fs),) 

## plot
plt.figure(figsize = (10, 4))
plt.plot(fs/fo, signal)
plt.show()

output_46_0

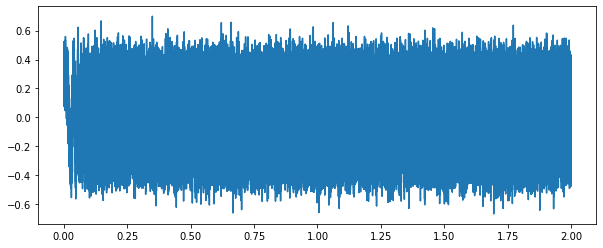
  • 첩 파형에 가우시안 잡음을 추가한 파형은 아래와 같습니다.

\begin{aligned}Noise&∼ N(0, 1^2)\\Signal(t)&= 0.3\cos(2 \pi f t^2) + Noise\end{aligned}

# Chirp wave
## sampling rate
N = 44100
fo = N
fs = np.arange(0, 2*N)

## signal
signal = 0.3 * np.cos(2*np.pi/3000000*fs**2) + 0.1 * np.random.randn(len(fs),) 

## plot
plt.figure(figsize = (10, 4))
plt.plot(fs/fo, signal)
plt.show()

output_49_0

Audio(signal.T, rate = fo)
  • 시각적으로 나타난 그래프에서는 잘 구별이 가지 않지만, 소리로 청취하는 경우 원신호와 잡음이 함께 식별되는 것을 확인할 수 있습니다.

2.3.4. 디락-델타 함수 (Dirac-delta function)

  • 디락-델타 함수는 이론물리학자 폴 디렉이 물리학에서 자주 사용하며 유명해진 함수로, 임펄스 함수라고 부르기도 합니다[8].

  • 디락-델타 함수는 충격 함수라고도 불리는데, $t=0$에서 무한대의 값을 갖고 그 이외 모든 시간에서 0 값을 가집니다[9].

  • 또한 디락-델타 함수를 적분했을 때 1이 된다고 정의하고 있습니다.

  • 이를 만족하는 디랙-델타 함수는 다음과 같습니다.

\[\begin{aligned} δ(t)&= \begin{cases} ∞,\;if\;t=0\\ 0,\;if\;t\ne 0 \end{cases} \\ \int_{-\infty}^{\infty} δ(t)\ \mathrm{d}t&=1 \end{aligned}\]

  • 충격 함수는 선별(sifting), 합성곱(convolution)과 같은 재미난 특성을 가집니다[9].

  • (합성곱 특성) 특히 어떤 함수이든 델타 함수와의 합성곱은 자기 자신이 됩니다. 다시 말해 충격 합수는 시스템의 단위 입력(unit input)이 되게 됩니다.

  • 그렇다면, 삼각 함수로 이러한 디렉 델타 함수, 임펄스 함수를 만들 수 있을까요?

  • 먼저 간단한 코사인 파형부터 시작하겠습니다.

theta = np.linspace(0, 6*np.pi, 2**8)
x1 = np.cos(theta)

# plot
plt.figure(figsize = (10, 3))
plt.plot(theta, x1)
plt.ylim([-1.1, 1.1])
plt.xlim([np.min(theta), np.max(theta)])
plt.xlabel(r'$\theta$', fontsize = 15)
plt.show()

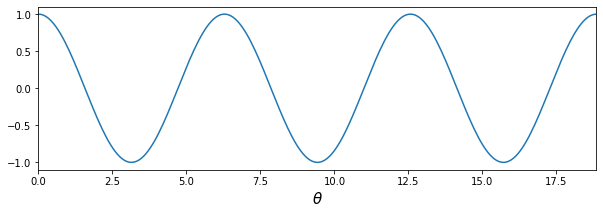
output_57_0

  • 아래와 같이, 코사인 함수의 주파수만 정수배하여 더해보겠습니다.

\begin{aligned} Signal(θ)&= \cos(θ) + \cos(2θ) + \cos(3θ) + \cos(4θ) \end{aligned}

x2 = x1 + np.cos(2*theta)
x3 = x2 + np.cos(3*theta)
x4 = x3 + np.cos(4*theta)

# plot
plt.figure(figsize = (10,9))
plt.subplot(3,1,1)
plt.plot(theta, x2/2)
plt.xlim([np.min(theta), np.max(theta)])
plt.ylim([-1.1, 1.1])

plt.subplot(3,1,2)
plt.plot(theta, x3/3)
plt.xlim([np.min(theta), np.max(theta)])
plt.ylim([-1.1, 1.1])

plt.subplot(3,1,3)
plt.plot(theta, x4/4)
plt.xlim([np.min(theta), np.max(theta)])
plt.ylim([-1.1, 1.1])
plt.xlabel(r'$\theta$', fontsize = 15)

plt.tight_layout()
plt.show()

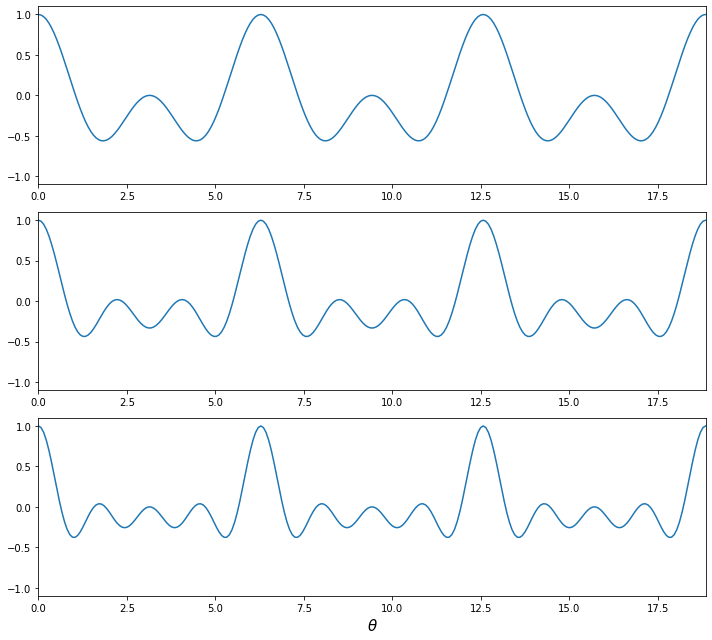
output_61_0

  • 특정 구간에서의 펄스를 제외하고는 0에 가까워지는 모습을 확인할 수 있습니다.

  • 그렇다면 다음과 같이 많은 정수배 코사인 파형을 더하게 되면 어떻게 되는지 확인해 보겠습니다.

\begin{aligned} Signal(θ)& = \sum_{i=1, 2, 3, ⋯}^{10000} \cos(nθ) = \cos(θ) + \cos(2θ) + \cos(3θ) + ⋯ \end{aligned}

x = np.zeros(theta.shape)

N = 10000
for n in range(1,N+1):
    x = x + np.cos(n*theta)

# plot
plt.figure(figsize = (10, 4))
plt.plot(theta, x/N)
plt.xlabel(r'$\theta$', fontsize = 15)
plt.ylim([-1.1, 1.1])
plt.show()

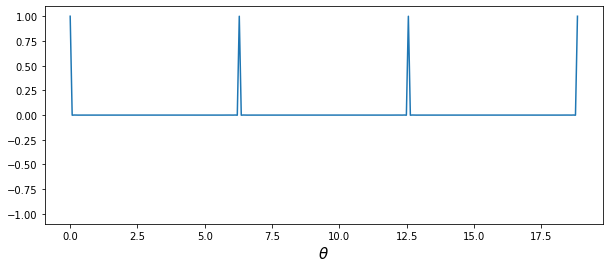
output_65_0

  • 위의 결과로부터, 무한히 많은 정수배 정현파 신호를 더하게 되면 결과 신호($Signal(θ)$)는 펄스가 반복되는 형상을 띔을 알 수 있습니다.

  • 아래와 같이, 무한한 펄스가 반복되는 형상을 디락의 빗(Dirac’s comb)라고도 부릅니다[10].

\begin{aligned} Signal(θ)&= \sum_{i=1, 2, 3, ⋯}^{∞} \cos(nθ) = \cos(θ) + \cos(2θ) + \cos(3θ) + ⋯ \end{aligned}

2.3.5. 정현파로 만드는 다양한 파형

  • 정현파를 합성해서 만들 수 있는 다양한 파형을 예제를 통해서 실습하도록 하겠습니다.
- 사각파 (square wave)

\begin{aligned} f(x)&= \frac{4}{\pi}\sum_{n=0}^{\infty} \frac{1}{2n+1}\sin((2n+1)x)\\Signal(θ)&= \sum_{i=1, 3, 5, ⋯}^{} \frac{4}{n\pi}\sin(nθ) = \frac{4}{\pi}\sin(θ) + \frac{4}{3\pi}\sin(3θ) + \frac{4}{5\pi}\sin(5θ) + ⋯ \end{aligned}

# sampling
N = 2**8
theta = np.linspace(0, 2*np.pi, N)
x = np.zeros(theta.shape)

# signal
for n in range(1, 12, 2):
    print(n)
    x = x + 4/(np.pi*n)*np.sin(n*theta)

# plot    
plt.figure(figsize = (10, 4))
plt.plot(theta/(2*np.pi), x)
plt.xlabel(r'$\theta/2\pi$', fontsize = 15)
plt.show()

1
3
5
7
9
11

output_71_1

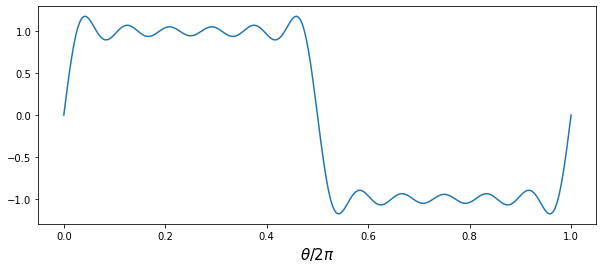
# sampling
N = 2**8
theta = np.linspace(0, 2*np.pi, N)
x = np.zeros(theta.shape)

# signal
for n in range(1, 5000, 2):
    # print(n)
    x = x + 4/(np.pi*n)*np.sin(n*theta)

# plot    
plt.figure(figsize = (10, 4))
plt.plot(theta/(2*np.pi), x)
plt.xlabel(r'$\theta/2\pi$', fontsize = 15)
plt.show()

output_72_0

# https://daewonyoon.tistory.com/258
def F(n, X):
    """
                   1
        F (t) = ------- sin ( (2n+1) t ) 
         n      2n + 1
    """
    return np.sin((2*n+1)*X)/(2*n+1)


def RectWave(n, X):
    """
          n
        Sigma  F (t)
         k=1
    """
    y = np.zeros(X.shape)
    for k in range(n+1):
        y = F(k, X) + y
    return y


X = np.linspace(-5, 5, 1000)
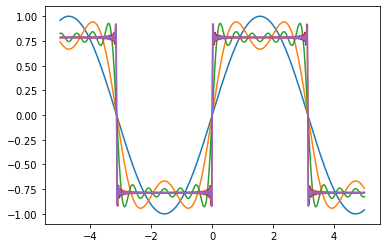
for i in (0, 1, 5, 50, 100):
    plt.plot(X, RectWave(i, X))
plt.show()

output_73_0

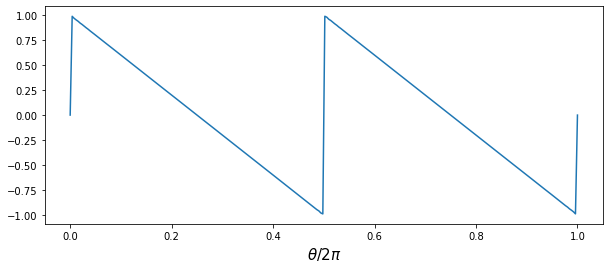
- 톱니파 (sawtooth wave)

\begin{aligned} f(x)&= \frac{4}{\pi}\sum_{n=1}^{\infty} \frac{1}{2n}\sin((2n)x)\\Signal(θ)&= \sum_{i=2, 4, 6, ⋯}^{} \frac{4}{n\pi}\sin(nθ) = \frac{4}{2\pi}\sin(2θ) + \frac{4}{4\pi}\sin(4θ) + \frac{4}{6\pi}\sin(6θ) + ⋯ \end{aligned}

# sampling
N = 2**8
theta = np.linspace(0, 2*np.pi, N)
x = np.zeros(theta.shape)

# signal
for n in range(2, 5000, 2):
    # print(n)
    x = x + 4/(np.pi*n)*np.sin(n*theta)

# plot    
plt.figure(figsize = (10, 4))
plt.plot(theta/(2*np.pi), x)
plt.xlabel(r'$\theta/2\pi$', fontsize = 15)
plt.show()

output_76_0

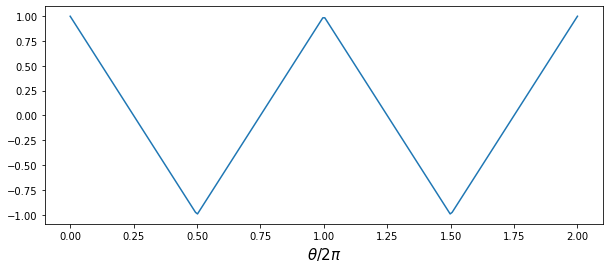
- 삼각파 (triangular wave)

\begin{aligned} f(x)&= \frac{8}{\pi^2}\sum_{n=0}^{\infty} \frac{1}{(2n+1)^2}\cos((2n+1)x)\\Signal(θ)&= \sum_{i=1, 3, 5, ⋯}^{} \frac{8}{(n\pi)^2}\cos(nθ) = \frac{8}{(1\pi)^2}\cos(1θ) + \frac{8}{(3\pi)^2}\cos(3θ) + \frac{8}{(5\pi)^2}\cos(5θ) + ⋯ \end{aligned}

# sampling
N = 2**8
theta = np.linspace(0, 4*np.pi, N)
x = np.zeros(theta.shape)

# signal
for n in range(1, 5000, 2):
    # print(n)
    x = x + 8/((np.pi*n)**2)*np.cos(n*theta)

# plot    
plt.figure(figsize = (10, 4))
plt.plot(theta/(2*np.pi), x)
plt.xlabel(r'$\theta/2\pi$', fontsize = 15)
plt.show()

output_79_0

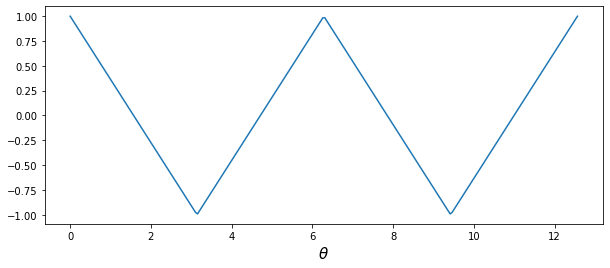
# plot    
plt.figure(figsize = (10, 4))
plt.plot(theta, x)
plt.xlabel(r'$\theta$', fontsize = 15)
plt.show()

output_80_0

  • 이번 실습을 통해서 정현파를 활용하여 수많은 파형을 생성해낼 수 있음을 확인하였습니다.

  • 더 많은 예제와 파형이 존재하지만, 이것을 끝으로 이번 실습을 종료하겠습니다. 사실은 시간이 부족해서…

3. 마무리하며 (Closing Remarks)

  • 결과 (Results)

    • 정현파와 여러 정현파를 합성하여 다양한 신호를 생성해 보았고, 직관적인 이해를 돕기 위해 소리로 청취하였습니다.

    • 시각적 & 청각적으로 파형을 확인하였으나, 하지만 정량적으로 어떤 성분이 구성된 파형인지 알 수 없었습니다.

  • 결론 (Conclusion)

    • 임의의 신호를 분해하여 구성 주파수 성분을 확인할 수 있는 방법이 필요합니다.

    • 아시는 분은 아시겠지만, 그 대표적인 해결책은 푸리에 변환(Fourier Transform)입니다.

    • 다음 DSP 포스팅에서는 푸리에 변환에 대해서 알아보고 실습하는 시간을 갖도록 하겠습니다.

4. 참고문헌 (References)

[1] IAI POSTECH Tutorials, “한국소음진동공학회 AI혁신위원회 2022년 인공지능 강습회 Discrete Signal Processing(DSP) 실습,” Link
[2] 골드문트의 (김포) 보청기, 오디오 RC 이야기, “샘플링 이론, 나이퀴스트 샘플링 레이트,” Link
[3] UNAQUENESS 트윗 셀프 아카이빙 블로그, “44,100HZ,” Link
[4] Wikipedia, “44,100Hz,” Link
[5] Wikipedia, “Chirp,” Link
[6] GoLook’s blog tistory blog, “ [IT] 가우시안 노이즈 (Gaussian Noise) & 백색잡음,” Link
[7] nittaku tistory blog, “python random 모듈 3개 정리 (randint, rand, randn),” Link
[8] Wikipedia, “디랙 델타 함수,” Link
[9] 영구노트 tistory blog, “디랙 델타 함수 (Dirac delta funtion),” Link
[10] 하루 naver blog, “물리학을 위한 미적분학[7-2]; 디락-델타 함수; 정의와 주요 성질,” Link

Etc…

  • 글에 설명과 수식이 상당히 많아졌습니다. 그에 비례해서 글 작성 시간도 매우 길어졌습니다… ㅜㅜ 수식 가운데 정렬을 할 줄 몰라서, 작업량 두배 시간도 두배 피버타임 겪었습니다… 난 바보인걸까…

  • 수식 중앙 정렬 문제를 해결할 방법을 찾았습니다! (2022-09-06)

    • 기존:
    $$\begin{aligned} ... \end{aligned}$$

    문제점: 원하지 않았던 “[ … ]” 기호가 프린팅 되었습니다.

    • 수정:
    \begin{aligned} ... \end{aligned}

    원하지 않았던 기호가 사라지고 중앙정렬만 깔끔하게 되었습니다!

  • 그래도 설명이 있는 편이 독자의 이해를 도울 것이라 생각합니다.

  • 더 열심히 하겠습니다! 부족한 부분 코멘트해주세요 (:

Shout-out to J. Choi !

댓글남기기

참고