5 분 소요

  • Author : Songho Lee
  • Date
    • First Published: September 01, 2022
    • Last modified: -

샘플링 이론 (Sampling Theorem)

시작하기에 앞서 (Before the beginning)

  • 파이썬을 활용한 샘플링 이론의 실습을 진행하겠습니다.

  • 조금 더 자세한 내용이 궁금하신 분들은 여기를 참고하시면 됩니다.

1. 서론 (Introduction)

  • 본 실습의 목적은 앞으로 포스팅될 내용(신호처리, 머신러닝 등)의 가장 기본이 되는 신호의 샘플링에 관한 것입니다.

2. 실습 (Practice)

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

2.1. 정현파 생성하기 (Generating sinusoidal wave)

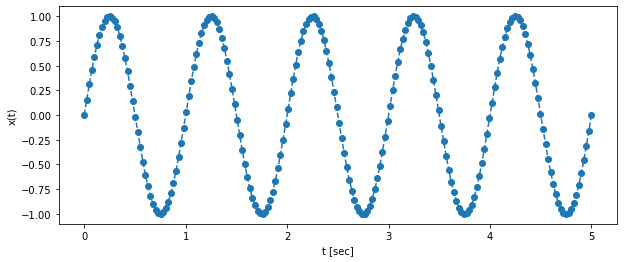
  • 간단하게 주파수($f$) 1 (= 주기($T$) 1, 주기는 주파수의 역수이므로) 이며, 그 진폭($A$)도 1인 사인파형을 생성해보겠습니다.
\[\begin{aligned} x(t)&=\sin(2\pi t) \end{aligned}\]

  • 생성한 사인파는 아래와 같습니다.

  • 아래와 같이 한 주기에 40개의 포인트를 샘플링하는 경우, 원래 의도했던 연속적인 사인파형을 잘 나타내는 것을 확인할 수 있습니다.

t = np.linspace(0,5,200)
x = np.sin(2*np.pi*t)

# plot
plt.figure(figsize = (10,4))
plt.plot(t, x, '--o')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.show()

output_10_0

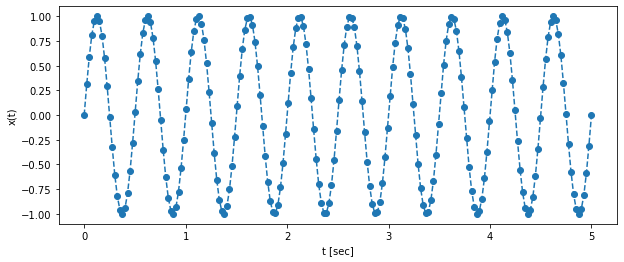
  • 이번에는 주파수($f$) 2 (= 주기($T$) 0.5) 이며, 진폭($A$) 1인 사인파형을 생성해보겠습니다.
\[\begin{aligned} x(t)&=\sin(4\pi t) \end{aligned}\]
  • 주파수가 1 일때와 마찬가지로 원래 사인파를 잘 나타내는 것을 아래의 결과에서 확인할 수 있습니다.
t = np.linspace(0,5,200)
x = np.sin(2*np.pi*2*t)

# plot
plt.figure(figsize = (10,4))
plt.plot(t, x, '--o')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.show()

output_14_0

2.2. 나이퀴스트 이론 (Nyquist frequency)

  • 나이퀴스트 이론이란, 신호는 그 신호에 포함된 가장 높은 진동수의 2배에 해당하는 빈도로 일정한 간격으로 샘플링하면 원래의 신호로 복원할 수 있다는 샘플링 이론입니다[2].

  • 아래의 예제를 통해 감을 잡도록 하겠습니다.

  • 2.1.에서 마지막으로 실습하였던 주파수 2인 사인파형을 생각해보겠습니다. 한 주기에 20개의 포인트를 샘플링하였고, 원래 파형을 잘 복원하는 것을 확인하였습니다.

  • 그렇다면 더 작게 샘플링하여도 원래의 파형을 잘 나타낼 수 있을까요?

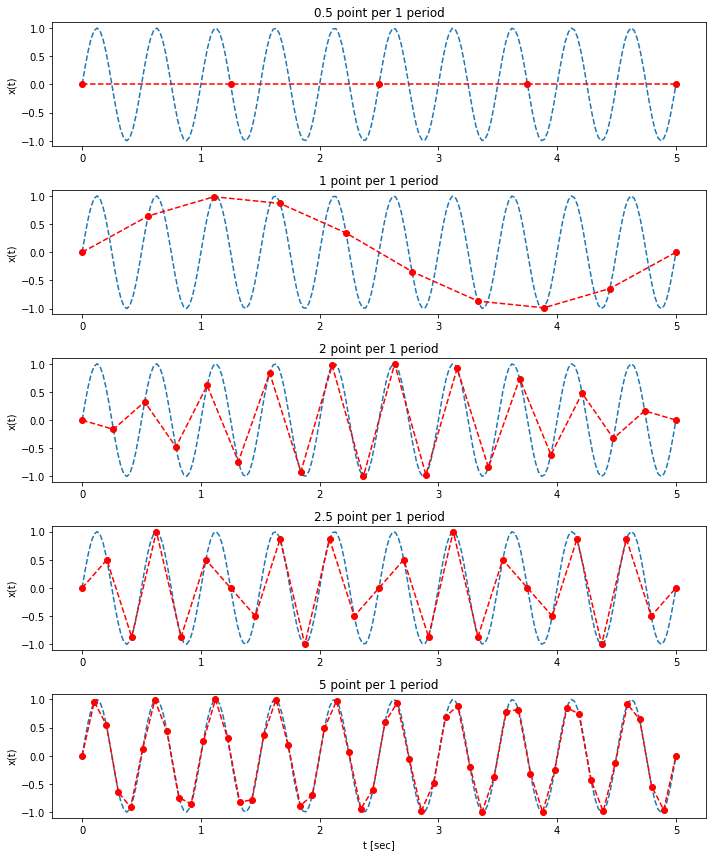
  • 한 주기에 0.5, 1, 2, 2.5, 5 개의 포인트만 나타내도록 하겠습니다.

t_1 = np.linspace(0,5,5)
x_1 = np.sin(2*np.pi*2*t_1)

t_2 = np.linspace(0,5,10)
x_2 = np.sin(2*np.pi*2*t_2)

t_4 = np.linspace(0,5,20)
x_4 = np.sin(2*np.pi*2*t_4)

t_5 = np.linspace(0,5,25)
x_5 = np.sin(2*np.pi*2*t_5)

t_10 = np.linspace(0,5,50)
x_10 = np.sin(2*np.pi*2*t_10)

  • 이해를 돕기 위해 원신호와 샘플링 포인트를 같이 나타내면 아래와 같습니다.

  • 한 주기에 0.5개, 1개 포인트만 샘플링한 경우, 원래 신호를 복원하지 못하는 것을 확인할 수 있습니다.

  • 한 주기에 2개 포인트 이상 샘플링한 경우, 주기성을 어느정도 복원하는 것을 확인할 수 있습니다.

  • 샘플링 포인트 갯수가 더 많아질수록, 신호를 더 잘 복원합니다.

# plot
plt.figure(figsize = (10,12))

plt.subplot(5,1,1)
plt.plot(t, x, '--')
plt.plot(t_1, x_1, 'r--o')
# plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.title('0.5 point per 1 period')

plt.subplot(5,1,2)
plt.plot(t, x, '--')
plt.plot(t_2, x_2, 'r--o')
# plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.title('1 point per 1 period')

plt.subplot(5,1,3)
plt.plot(t, x, '--')
plt.plot(t_4, x_4, 'r--o')
# plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.title('2 point per 1 period')

plt.subplot(5,1,4)
plt.plot(t, x, '--')
plt.plot(t_5, x_5, 'r--o')
# plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.title('2.5 point per 1 period')

plt.subplot(5,1,5)
plt.plot(t, x, '--')
plt.plot(t_10, x_10, 'r--o')
plt.xlabel('t [sec]')
plt.ylabel('x(t)')
plt.title('5 point per 1 period')

plt.tight_layout()

output_19_0

  • 하지만 연속적인 아날로그 신호를 복원하기 위해 무한정 샘플링할 수 없습니다.

  • 이를 보완하는 이론이 바로 나이퀴스트 이론입니다[3, 4].

  • 아날로그 신호를 디지털화(Analog to Digital Convertion)하는 과정에서, 샘플링된 신호에 가까운 범위를 대표하는 정수값으로 바꾸는 양자화(Quantization) 과정을 거칩니다.

  • 양자화 과정에서 양자화 오차가 발생하여 기존 아날로그 신호와는 차이가 존재하는 신호를 얻게 됩니다.

  • 하지만 나이퀴스트 샘플링 레이트가 만족되면 이론상으로는 오리지널 신호가 복원이 되는 것입니다.

  • 신호를 복원했을 때 기존 아날로그 신호의 유실 없이 복원하기 위해서 얼마만큼 신호를 샘플링해야 하는가에 대한 것이 나이퀴스트 주파수입니다.

  • 서두에서 언급하였듯, 나이퀴스트 이론에 따르면 원래 신호를 복원하기 위해서는 그 신호에 포함된 가장 높은 진동수의 2배 이상으로 샘플링해야 합니다.

2.3. 에일리어싱 (Aliasing)

  • 에일리어싱이란 나이퀴스트(Nyquist) 샘플링 레이트(sampling rate) 보다 실제 샘플링 레이트가 충분히 빠르지 못할 때 생기는 현상입니다[5].

  • 주파수 도메인에서 스펙트럼이 겹쳐지는 바람직하지 못한 현상입니다.

  • 에일리어싱 예시 1 - 시계[5]
    • 시계 초침은 1분에 한바퀴 회전합니다.
    • 눈을 감고 15초마다 눈을 떠서 쳐다보면, 1분에 4번을 보게 되고, 초침이 도는 방향과 회전속도를 유추할 수 있습니다. (= 1분에 시계방향으로 1바퀴 유추 가능)
    • 30초마다 눈을 떠서 쳐다보면, 초침이 도는 방향을 알기가 모호해집니다. 이 한계점이 나이퀴스트 레이트입니다. 1분에 두번보다 더 자주 보아야 방향과 회전속도를 알 수 있습니다.
    • 만일 45초마다 보게 되면, 45×4=180초, 즉 2분마다 반시계 방향으로 1바퀴 도는 것처럼 보일 수 있습니다.
    • 만일 75초마다 본다고 하면, 75×4=300초, 즉 5분마다 시계방향으로 한 바퀴 돈다고 생각하게 됩니다.
    • 즉, 1분에 2회 이하로 느리게 보게 되면 원래의 회전 방향과 속도를 맞힐 수 없습니다.
  • 에일리어싱 예시 2 - 마차 바퀴 현상 (Wagon-wheel effect)[1, 6]
    • 카메라가 마차 바퀴를 30 fps(frame per second)로 영상을 촬영합니다.
    • 마차 바퀴가 1초에 한 바퀴씩 돈다면, 12도에 한번씩 30번 샘플링이 되어 무리없이 바퀴가 돌아가는 모양의 영상이 촬영됩니다.
    • 마차 바퀴가 1초에 30 바퀴씩 돌아간다면, 바퀴는 항상 정확히 같은 모양으로 있게 된다.
    • 마차 바퀴가 1초에 30 바퀴 보다 조금 느리다면, 바퀴가 덜 돈 상태로 찍혀 바퀴가 ‘뒤로 도는 듯한’ 영상을 얻게 됩니다.
    • 마차 바퀴가 1초에 30 바퀴 보다 조금 더 빠르다면, 바퀴가 더 돈 상태로 찍혀 바퀴가 ‘느리게 앞으로 도는 듯한’ 영상을 얻게 됩니다.
  • 유독 자동차 바퀴에서 이런 현상이 도드라지게 나타나는 이유?
    • 자동차 휠은 일정한 각도를 가지고 바깥으로 퍼져나가는 형상이기 때문에 한바퀴를 돌 때 여러번 같은 장면이 반복된다.
    • 따라서 한 바퀴 도는 동안 비슷한 장면이 반복되고, 한 바퀴에 5번 동일한 모양이 나타난다면, 1초에 6바퀴 돌더라도 정지한 것처럼 보일 수 있다.
%%html
<center><iframe 
width="560" height="315" src="https://www.youtube.com/embed/jHS9JGkEOmA?rel=0" frameborder="0" allowfullscreen>
</iframe></center>
  • 에일리어싱 예시 3 - 공중부양 하는 새
    • ㅋㅋ 웃깁니다.
%%html
<center><iframe 
width="560" height="315" src="https://preview.redd.it/aimf202bk7l01.gif?format=mp4&s=9bc22cb5ae05b22d6ba9bdc216d228dab678be22" frameborder="0" allowfullscreen>
</iframe></center>
  • 에일리어싱 예시 4 - 화질 깨짐
    • 해상도가 낮은 그림을 원본 이상으로 확대할 경우 문제가 생깁니다.
    • 한 변의 길이를 2배로 늘린다면 한 점은 4개의 점이 되겠죠? 이 때 확대 전 1개의 픽셀이 가지고 있던 색을 4개의 픽셀에 똑같이 칠해버리는 경우 문제가 생깁니다.
    • 예를 들어 비스듬이 그린 직선을 확대한 경우, 직선이 아닌 계단 모양이 나타납니다.
    • 해결 방법: 안티 에일리어싱(이에 대한 것은 여기에서는 다루지 않겠습니다.)

3. 마무리하며 (Closing Remarks)

  • 결과 (Results)
    • 나이퀴스트 샘플링 레이트에 따라서, 기존 신호 최고 주파수의 두 배로 샘플링을 한 경우, 시간 영역(Time-domain)에서의 어느 정도 주기적인 양상은 나타내는 것을 확인하였습니다.
    • 하지만 2배의 샘플링으로는 Time-domain 신호의 완벽한 복원은 어려움을 확인하였습니다.
    • 시간 영역(Time-domain)과 주파수 영역(Frequency-domain)에 대한 것은, 이후 Fast Fourier Transform(FFT) 포스팅에서 다시 다루도록 하겠습니다.
  • 결론 (Conclusion)
    • 이렇게 해서, 아날로그 신호를 분석하기 이전에 신호를 샘플링하는 부분을 살펴보았습니다.
    • “그냥 무조건 샘플이 많을수록 좋은거네,” 라고 생각할 수 있습니다.
    • 하지만 샘플이 많을수록 버퍼에 들어가는 데이터의 용량이 커지고 메모리가 더 소요되니, 시스템에 맞는 적절한 샘플링을 설정하는 것이 중요합니다.
    • 저를 포함한, 자연 현상 및 아날로그 신호를 측정하고자 하는 사람들에게 조금이나마 도움이 되었으면 합니다.

4. 참고문헌 (References)

[1] IAI POSTECH Tutorials, “한국소음진동공학회 AI혁신위원회 2022년 인공지능 강습회 Discrete Signal Processing(DSP) 실습,” Link

[2] ralasun github, “나이퀴스트 이론(Nyquist frequency),” Link

[3] 가상현실 공간의 사운드 디자인 VR Sound, “나이퀴스트 이론, 샘플링 레이트,” Link

[4] 골드문트의 (김포) 보청기, 오디오 RC 이야기, “샘플링 이론, 나이퀴스트 샘플링 레이트,” Link

[5] 골드문트의 (김포) 보청기, 오디오 RC 이야기, “오버샘플링, 업샘플링, 에일리어싱,” Link

[6] 이웃집과학자, “차 바퀴 휠이 왜 뒤로 돌지?! ‘에일리어싱’,” Link

[7] reddit, “Framerate synced with a bird’s wings,” Link

Etc…

  1. 포스팅 공약을 했건만 지켜지지 못했군요… 아직 많이 부족함을 느낍니다.

  2. 부족한 부분 코멘트해주세요 (:

  3. 수식 가운데 정렬하는 마크다운 문법이 ‘\(...\)’ …에 수식을 삽입하는 것이 아닌걸까요… 왜 안되는 걸까요… ): 어렵네요 ㅠ.ㅠ

Shout-out to J. Choi !

댓글남기기

참고